Breaking a poorly implemented password recovery

05 Aug 2025

Enumeration
Some math
Probabilities
More probabilities
Expected value
Exploitation
Preventing this attack
Public logs
Verbose notifications
Flawed recovery verification

The TryHackMe machine Hammer contains a poorly implemented password recovery feature that can be exploited to gain a foothold on the system. Here I'll share how to hack into the first part of the challenge, what makes it possible, and how to prevent attacks like this in your systems.

Note

This is not intended to be a write-up for this challenge. Therefore, there are many places you will need to fill in the spaces.

Enumeration

After the initial enumeration of ports, we get to a webapp in port 1337, with a login page with a Forgot your password? link in it.

2025-08-04-165751-hyprshot — Forgot password form. Notice the notification that gives away information about the existence of a user with certain email.

With a little more enumeration, we find some logs that have some interesting data, like the possible existence of a user with email tester@hammer.thm. This is confirmed with the password recovery form:

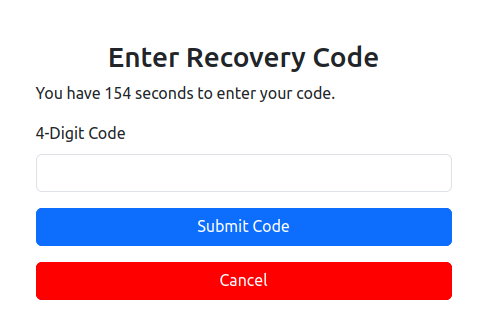
2025-08-04-171015-hyprshot — Password recovery code form.

They are asking for a 4-digit code to reset the password, and as you can see from the screenshot, the page has a countdown; this is the (formatted) code for it:

.jslet countdownv = 180;
function startCountdown() {
  let timerElement = document.getElementById("countdown");
  const hiddenField = document.getElementById("s");
  let interval = setInterval(function () {
    countdownv--;
    hiddenField.value = countdownv;
    if (countdownv <= 0) {
      clearInterval(interval);
      //alert("hello");
      window.location.href = "logout.php";
    }
    timerElement.textContent =
      "You have " + countdownv + " seconds to enter your code.";
  }, 1000);
}

The page gives you 3 minutes to input the code before redirecting you to the logout page. Of course, this gives no security at all, as one can very easily modify the countdownv variable in the console or clear the interval set to update the count.

As I started trying values by hand, after a few requests, I got blocked and couldn't make any requests. I noticed that the blocking was tied to the value of the PHPSESSID, after removing it, the blockade was lifted.

The request set the header Rate-Limit-Pending: 9, which started with a value of 9 and decreased by one every time a request was made with the same session ID. When the value got to 1, I'd get blocked on the following request.

This means that I can try up to 9 different code values before I need to update to a new session ID and start over. Maybe I can do a brute-force attack.

Some math

Before starting to dump more carbon dioxide into the atmosphere with our inherently inefficient brute-force attack, it's worth asking ourselves if this makes sense. Is it possible to find the code within a reasonable time? To answer that, we need to answer another question: How many times on average should I try to guess the code before I succeed?

I'll take some time here to derive some formulas for probabilities to answer this question.

Probabilities

First of all, let's assume that the generated code is picked at random with a uniform probability distribution from $0000$ to $9999$ . This means, there's a probability $p = 1/N$ (with $N = 10^4$ ) that any of the possible 4-digit numbers is the code we are looking for.

If, given that the code is picked and fixed, we guess it is any 4-digit number, the probability that we are right is $p$ . If we now try again with another number, the probability of getting it right is, again, $p$ .

Important

It is fundamental that we are clear about this. Every guess is an independent event, and they do not affect the probabilities of each other.

Of course, the probability of having guessed the code after two tries is greater than the probability of having guessed it in only one try. But beware of the distinction between "the probability of having guessed after two tries" and "the probability of guessing in the second try". This may be a subtle distinction for people unfamiliar with probability, and is the source of many misunderstandings.

Here are two properties of the probabilities of independent events that will be helpful in the following:

Given two independent events $A$ and $B$ , with probabilities $P(A)$ and $P(B)$ respectively;

the probability of any of the two happening is equal to the sum of the probabilities $P(A \cup B) = P(A) + P(B)$ .

The probability of the two events happening is equal to the product of the probabilities $P(A \cap B) = P(A)P(B)$

With that in mind, let's break down the probability of guessing the code within two tries. There are two ways in which we could have guessed the code: in the first try and in the second try, and the probability of guessing in any of the two is the sum of those.

The first probability is easy, it's just $1/N$ . The second one needs a little more attention. We will be smart when guessing, so we will not choose the same number twice; then, the independent probability of guessing correctly the second time will be $1/(N-1)$ .

Now, for the correct guess to be the second one, two conditions must be met: we must not have guessed correctly in the first try, and we must guess correctly in the second one. So, the probability of this is the multiplication of the probabilities of the two conditions¹:

$\frac{1}{N-1}\left(1 - \frac{1}{N}\right) = \frac{1}{N}$

With this, we get that the probability of having guessed the code after two tries is $2/N$ . This result can be generalized, and the probability of having guessed the code after $n$ tries is

$P(x \leq n) = \frac{n}{N}$

Notice the notation. I'm using $x < n$ as a way to express that this is the probability of guessing correctly in any of $n$ tries, and that

$P(x \leq n) = P(x = 1) + P(x = 2) + \dots + P(x = n)$

where $P(x = y)$ is the probability that the correct guess happens in the $y$ -th try.

Important

I can't stress this enough. Notice the distinction between "guessing in the $x$ -th try" and "the correct guess happens in the $x$ -th try". The former refers to a single event, whereas the latter involves multiple events.²

Notice that the probability can't be greater than $1$ , so if $n \geq N$ , the probability is $1$ , i.e., we are certain that we guessed the code because we tried every possible number.

More probabilities

Note

I will be reusing the variables $n$ , $p$ , and $P$ . Threat this section and the previous as independent scopes. Sorry for the confusion it might create.

Back to our problem, we know³ we have $n = 9$ tries to guess the code before we are blocked. After that, we need to start over, because a new code is generated. We can group our guesses in batches of $n$ each, where the probability of guessing the code in a batch is $p \equiv n/N$ . These batches are independent of each other if we keep our assumption that a random code is generated each time.

So, what's the probability of having guessed the code after $n$ batches? This is more easily calculated as the opposite of not having guessed the code after $n$ batches:

$P(x \leq n) = 1 - (1-p)^n$

Let's break that down: the probability of guessing in a batch is $p$ , then the probability of not guessing is $1 - p$ ; not guessing after $n$ batches requires not having guessed in any of the $n$ batches, so the probability is the product of the independent probabilities: $(1 - p)^n$ . Finally, the probability of guessing in any of the $n$ batches is the complement of the previous, hence the equation above.

This is not to be confused with the probability of guessing in the $n$ -th batch. As before, these are independent events, so the probability remains $p$ . Also, not to be confused with the probability that the correct guess happens in the $n$ -th batch, this probability is the product of the probability of guessing in the $n$ -th batch and the probability of not having guessed until then:

$P(x = n) = p \cdot \left(1 - P(x \leq n - 1)\right) = p (1 - p) ^{n - 1}$

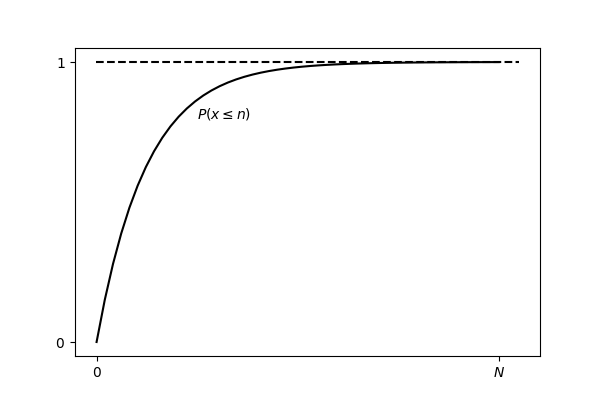
Below is shown the graph of $P(x \leq n)$ . It approaches asymptotically $1$ but never reaches it. So, what was the point of all of this? The probability on its own is not very useful; we need another number: the expected value of the number of batches that need to be tried before guessing correctly.

Plot of P vs. n — Plot of the relation between the probability of guessing correctly and the number of tries. The probability approaches asymptotically 1 but never reaches it.

Expected value

The expected value $E[X]$ of a random variable $X$ is a weighted average of the values the variable can take, where the weights are the probabilities of each value.

$E[X] = \sum_i X_i \cdot P(X_i)$

As the name suggests, it gives a sense of what value one should expect when obtaining a random value of $X$ . In our problem, we are interested in the expected value of the number of batches to try for us to have a correct guess of the code:

$E[n] = \sum_{n = 1}^{\infty} n \cdot P(x = n)$

This is the weighted sum of $n$ with the probability that the code is guessed in the $n$ -th try. Using the equations from above, the expression becomes:

$\begin{align*} E[n] &= \sum_{n = 1}^{\infty} n \cdot p (1 - p)^{n - 1} \\ &= p \sum_{n = 1}^{\infty} n (1 - p)^{n - 1} \\ &= p \sum_{n = 1}^{\infty} n (1 - p)^{n}(1 - p)^{- 1} \\ &= \frac{p}{1 - p} \sum_{n = 1}^{\infty} n (1 - p)^{n} \end{align*}$

To get the result, let's derive the value of the summation

$\begin{align*} S(k) &= \sum_{x = 1}^{\infty} x k^x \\ &= \lim_{n \to \infty} \sum_{x = 1}^{n} x k^x \\ &= \lim_{n \to \infty} S(k, n) \end{align*}$

Click here to see the derivation

We have the partial sum

$S(k, n) = \sum_{x = 0}^{n} x k^x$

Multiplying each side by $k$ we get

$S(k, n) \cdot k = \sum_{x = 0}^{n} x k^{x + 1}$

Then we can make the substitution $z = x + 1$ , which lets us with

$\begin{align*} S(k, n) \cdot k &= \sum_{z = 1}^{n + 1} (z - 1) k^z \\ &= \sum_{z = 1}^{n + 1} z k^z - \sum_{z = 1}^{n + 1} k^z + k^0 - k^0 \\ &= \sum_{z = 0}^{n + 1} z k^z - \sum_{z = 0}^{n + 1} k^z + 1 \\ &= S(k, n) + k^{n + 1}(n + 1) - \sum_{z = 0}^{n + 1} k^z + 1 \\ S(k, n) \cdot (k - 1) &= k^{n + 1}(n + 1) + 1 - \sum_{z = 0}^{n + 1} k^z \end{align*}$

Let's solve the summation in the equation above:

$\begin{align*} Q(k, n) &= \sum_{x = 0}^{n} k^x = 1 + k + k^2 + \dots + k^n \\ Q(k, n) \cdot k &= \sum_{x = 0}^{n} k^{x + 1} \\ &= k + k^2 + k^3 + \dots + k^{n + 1} + 1 - 1 \\ &= 1 + k + k^2 + k^3 + \dots + k^{n} + k^{n + 1} - 1 \\ &= \sum_{x = 0}^{n} k^x + k^{n + 1} - 1 \\ &= Q(k, n) + k^{n + 1} - 1 \\ Q(k, n) \cdot (k - 1) &= k^{n + 1} - 1 \end{align*}$

$\boxed{Q(k, n) = \frac{k^{n + 1} - 1}{k - 1}}$

With this result, our original summation becomes

$\begin{align*} S(k, n) \cdot (k - 1) &= k^{n + 1}(n + 1) + 1 - \frac{k^{n + 2} - 1}{k - 1} \\ &= \frac{k^{n+2}(n + 1) - k^{n + 1}(n + 1) + k - 1 - k^{n + 2} + 1}{k - 1} \\ &= k\frac{k^{n+1}n - k^{n}(n + 1) + 1}{k - 1} \end{align*}$

$\boxed{S(k, n) = \frac{k}{(k - 1)^2} \left( k^{n+1}n - k^{n}(n + 1) + 1 \right) }$

Finally, applying the limit when $n \to \infty$ , and because $k < 1$ :

$\boxed{S(k) = \frac{k}{(k - 1)^2}}$

Subtituting $k = 1 - p$ for our problem we get

$E[n] = \frac{p}{1-p} \frac{1 - p}{p^2}$

$\boxed{E[n] = \frac{1}{p} }$

Let's interpret this result. If we substitute $p = n / N$ we get

$E[n] = \frac{N}{n}$

batches. But in each batch we try $n$ times, so the expected number of individual attempts is $N$ .

This result seems very intuitive. In fact, this was my first guess long before even considering deriving the probabilities and expected value. What this result tells us is that, on average, if the code is a random number chosen each time from $N$ possible values, we should try to guess it $N$ times before getting it right.

Don't confuse this with the situation of a fixed code and $N$ guesses. In that situation, we are guaranteed to be right in the $N$ -th guess or before, then the expected value would be less than $N$ .

Exploitation

Note that in the previous interpretation of the result, the number of requests per batch gets cancelled out, so, in theory, it's irrelevant how many attempts per PHPSESSID we make. However, each attempt requires a request to be made to the website, and for each session ID, a new request needs to be made to get it. So, we should use the 9 requests allowed by each PHPSESSID if we want to take the least time to crack the code.

From the result, we also get that we will need, on average, 10000 attempts. If we made all the requests sequentially, and if every one of them took 100 ms, we would spend ~17 minutes until we cracked the code. In my experience with the machine, the requests took more than 100 ms each, so this approach is not desirable.

To speed this up, we can make concurrent requests to the server, therefore multiplying the attack speed. In crack.py, you can see the code I made to crack the pin. I used aiohttp instead of requests to make the requests concurrent. This is only one of many possible approaches; I could have made concurrent sessions as well to speed up the attack even more, but this was good enough to run within 20 seconds.

Also, notice that I used 8 requests per session instead of 9, because I need the potentially last request to fill the password reset form.

Preventing this attack

This application had three vulnerabilities that allowed us to exploit it. Let's see them and discuss how to prevent them.

Public logs

First of all, we were able to see logs of the system unauthenticated and without any authorization. The logs may contain sensitive information, like usernames, emails, or even passwords. So, make sure that your logs are not accessible to the public.

Verbose notifications

The next piece to get the email we used was exploiting the information given in the Forgot Password form. When the email entered was not in the database, there was an error message that told us. This can be used to check if an email is registered on the website, enumerating from a wordlist. In our case, we were able to validate that the email found in the public logs was registered on the website.

The takeaway of this story is to be careful about the information you give back to the user; it might seem harmless, but give away enough information for hackers to use.

Flawed recovery verification

Finally, using a 4-digit code to verify the authenticity of a password reset is not strong enough. As we saw, the expected number of attempts is only $10^4$ , and brute-forcing it is feasible. By adding only two more digits and including letters in the code, the time of the attack increases by more than 256,000 times. That's almost 3000 years with the same speed of tries per second.

Always make these calculations before implementing your authentication. The security of the Internet relies on brute-force to take astronomically large times when no information is given.

Also, blocking based on the PHPSESSID is not robust enough, as we saw, we can simply get a new one. Blocking or throttling by IP address would be a better approach to prevent brute-force attacks.

The probability of an event not happening is $1 - p$ , where $p$ is the probability of the event happening.

I apologize if my writing makes these subtle differences even more difficult to distinguish.

Actually, we don't know this. We assume that a single code is generated for every PHPSESSID, and we can try many times to guess the same code until we get blocked.